Minecraftで演算回路を理解してみる[1/2]
目次
・はじめに
はじめまして。12/21, 12/22アドカレ担当、RiG++2回生、コーディング課のHayatoIといいます。
普段部室にもあまり居ないので部内の人でもはじめましての人多いかも。
さて、今年のテーマは「今、おすすめしたいこと」です。ということで、私がおすすめしたいことはこちら。

はい。Minecraftという名の論理演算シュミレータです。誰もが知っているビッグタイトルであるMinecraft、マイクラですがこのゲーム実は何でもできちゃうんですよね。
大学入る前までは建築など”まとも”に遊んでいたのですが、大学に入ってからおかしなことに私のマイクラは論理回路のシュミレータと化してしまいました。このマイクラ、論理回路を視覚的に確認することができるのでとっても回路の理解に役立つんですよね。1回生のとき論理回路や計算機科学の授業の理解に重宝しました。ということで、様々な演算回路をMinecraftで作ってみて、理解を深めながらMinecraft論理演算シュミレータの良さについて2日間にわたって語っていこうと思います。
あと、今回は普段学んでいる回路をマイクラで作成することで視覚的、そして直感的に理解していくことに焦点を当てるのでマイクラに関する知識は基本的に省略していきます。マイクラなんて調べればいくらでも出てくるしね。
・対象
・基本的な論理回路(ANDやORの真理値表くらい)を知っている人
・(ある程度)2進数を扱える人
・マイクラの知識は無くてもOK
くらいの人を想定して書きました。ある程度知ってるよーって人は復習用にでもしてください。乗算除算とか意外と忘れてるかも??
・目標
マイクラを通じて以下の回路について理解を深めよう
・基本的な論理回路 (AND や OR)
・四則演算回路
・エンコーダ、デコーダ
・目次
——–1日目———-
・レッドストーンについて
・基本的論理ゲートの実現
・2進数と半加算器
・全加算器による加算回
・補数の扱いについて
・補数と加算による減算の実現
———2日目———-
・筆算の考え方と乗算回路
・除算回路
・エンコーダ、デコーダによる2⇔10進数変換
・レッドストーンについて
さて、実際に論理回路を作成する前に、まずはマイクラのレッドストーン回路について話さないといけないですね。大体の人がもう知ってると思いますがマイクラには”ほぼ”論理回路のように扱えるレッドストーンというものがあります。普通はゲーム内でランプ光らせたり、ピストンというレッドストーンの信号によって動くものを使って自動ドア作ったりなんかしますが、ある程度論理回路の知識があれば電卓などを作る猛者もいます。今回はこのレッドストーンを用いてその電卓を部分的に作っていきましょう。
今回の作成にあたって最低限知っておいてほしいマイクラのアイテムは以下の通り。
マイクラの知識ある人は読み飛ばしてもらってOK
・レッドストーン

これが無いと何も始まらない。ON(赤く光っている)、OFF(光っていない)状態を持ち、接続しているレッドストーンに信号を伝えることができる。論理回路で言うと信号線。
少し細かく話すとマイクラのレッドストーンはONOFFだけでなく信号の強度といって16段階の信号の強さがあります。これ応用すればA/D or D/Aコンバータとかも作れそうだけどマイクラの仕様上、1ブロック分離れるごとに信号の強さが1弱まるので実用的ではなさそう。多分。
・レバー
ONとOFFの状態を切り替え、保持することができる。
・レッドストーンランプ

隣接するブロックにONの信号があると光ります。今回はON、OFFの状態を視覚的にわかりやすくするために使います。
・リピータ

主に2つ役割があります。1つ目は名前の通りで信号を延長します。レッドストーンは16ブロック分までしか伝わらないので、中間にリピータを挟んで信号を延長する必要があります。
2つ目はトランジスタです。半導体ですね。一定方向から来た信号しか通さなくなります。電気回路と論理回路が混ざって若干ややこしい。
ただこのリピータですね、一つ挟むごとに0.1秒という情理民驚愕の遅延がございます。逆手に取ってクロック回路とか作る人も居ますが、基本的にいわゆる”マイクラガチ勢”の人はこの遅延を少なくするために日々リピータの削減に励んでいるそうです。
マイクラを知らない人はこれくらい覚えておけば大丈夫です。XOR回路でコンパレータというアイテムを多用しますが結構仕組みが複雑なので今回は「そういうもの」程度でOK。
・基本的論理ゲートの実現
では、ある程度レッドストーンについて理解したところで早速基本的な回路を作成していきましょう。真理値表とMIL記号もついでに載せときます。真理値表の0と1は、1がON、つまりランプが光っている、0はOFFでランプが消灯している状態を表しています。マイクラでの結果がちゃんと真理値表通りになっているか確認しながら理解を深めていきましょう。
・NOT

NOT回路はこのように作ることができます。紹介していないアイテムがありますが今回は論理回路を理解する手段としてのマイクラなので気にしない気にしない。
レバーがONのときは出力がOFFになってレバーOFFのときは出力ONになっていることが確認できますね。
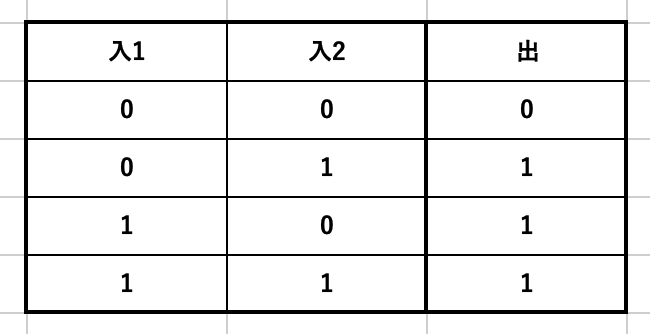
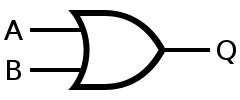
・OR

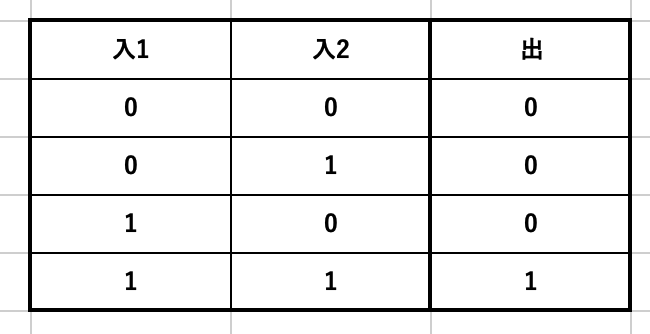
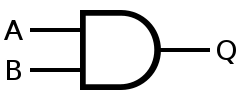
・AND

基本となる論理演算3つです。ここまでは恐らく大丈夫かな。
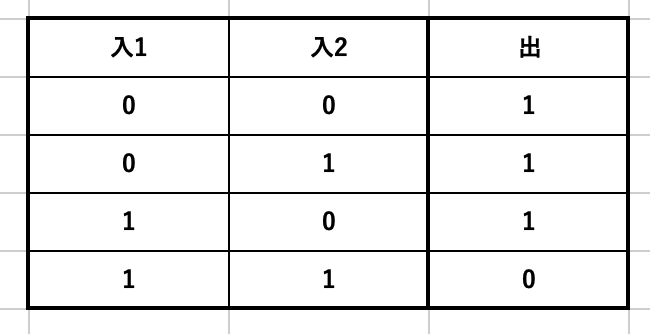
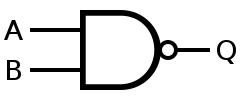
・NAND

ANDにNOT繋げるだけ。ですが意外と重要です。
いざ紙の上での計算となると意外とこんがらがります(0になる条件で考えてしまうとNORと逆になってしまう)。真理値表しっかり見て間違わないようにここで理解していってください。
余談ですが、NAND回路だけを用いることですべての基本的な論理回路を作ることができることがわかっています(完全系)。例えばANDを作りたい場合は以下のようにすればつくることもできます。
「複雑になるだけじゃん」と言われそうですが、コストの面で見ると意外と良かったりします。現実世界ではこの手法が基本回路の種類を減らしてコストカットすることに役立ってるらしい。NANDは何度も使います。
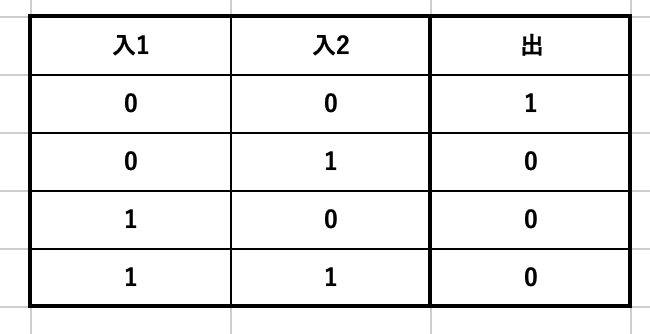
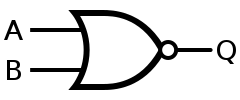
・NOR

NAND同様こっちはORにNOTつけただけ
・XOR

排他的論理和。排他的経済水域じゃないですよ。
これ意外とややこしいですね。真理値表をしっかり覚えましょう。マイクラでの実装も少し難しいです。
紹介はしなかったんですが、コンパレータというアイテムを使うとより省スペースでXOR回路を作ることができます。
現実世界では3路スイッチなどにこっそり使われてたりします。例えば家の階段。真理値表からわかるように、片方のスイッチを操作した時、もう一つのスイッチの状態に関わらず出力が変化することがわかりますね。この性質を利用して階段をのぼるとき、1階でつけた階段の電源が2階のスイッチで消すことができる訳ですね。
結果は同じなんですが、マイクラでの実装(スペースなどの関係)のため以下のようなXOR回路も使用していきます。

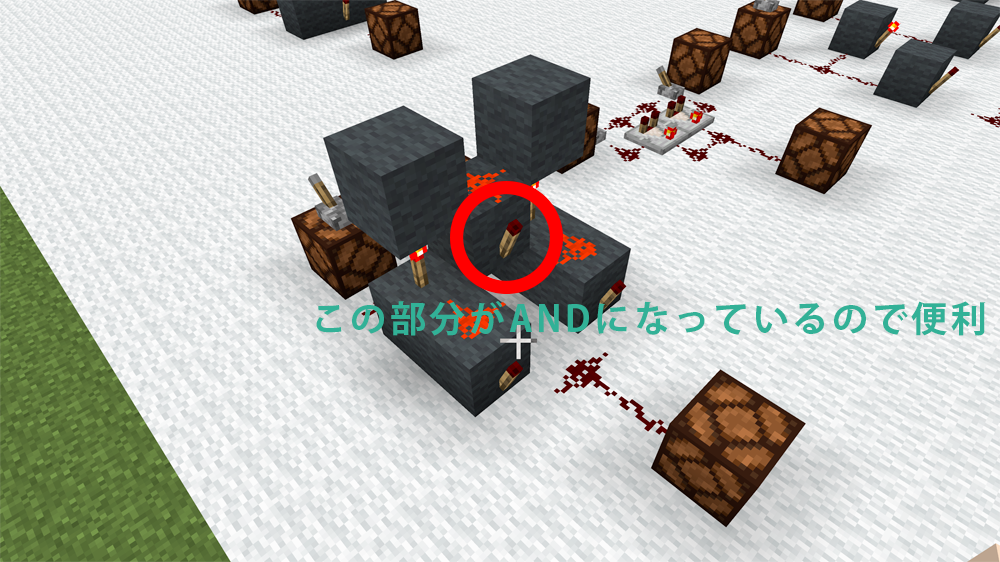
スクリーンショットに文字入れるの面倒だったので次からは手書き
・2進数と半加算器
ここで2進数の復習でもしておきましょう。
ご存知の通りコンピューターは0と1の2つの状態の組み合わせたものしか扱うことができません。もちろんマイクラのレッドストーンもONとOFFの2状態しか持たないので2進数で扱う必要がありますね。なのでコンピューター上で四則演算を実現しようとした時、我々の世界では10進数を扱っているため、2進数に変換してから計算させてあげる必要があります。
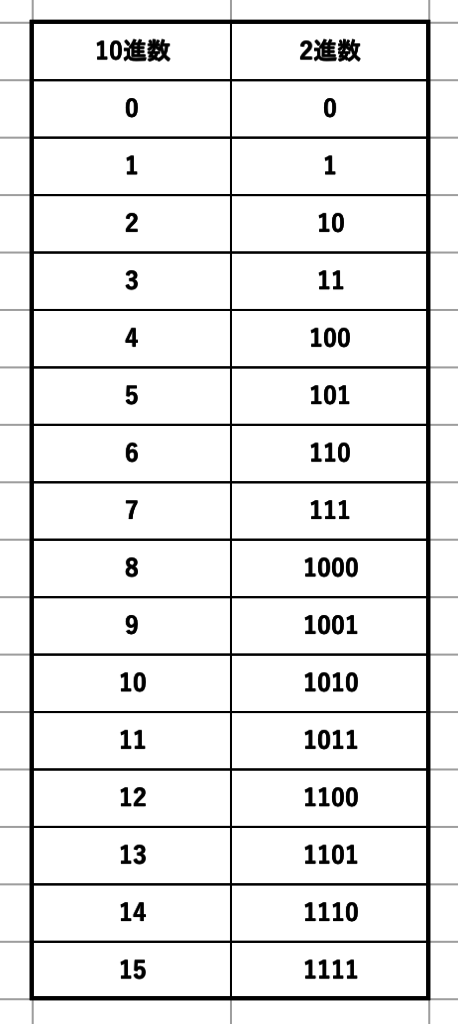
一応簡単に10進数と2進数の対応表を載せときます。補数の話やマイクラでの10⇔2進数変換(デコーダ、エンコーダ)は後ででてきます。
さあ、では早速先程学んだ回路を組み合わせてまずは加算器を作ってみましょう。
加算器は半加算器、全加算器の2種類に分けることができます。これらの違いは下位桁からの繰り上げも入力とするかどうかです。まずは簡単な半加算器からいきますね。
作成に移る前に、まずは2進数の足し算の結果について見てみましょう。入力はそれぞれ先程と同様にONかOFFの1ビットが2つあります。全部で4通りです。一方で、出力は1つでは無いですね。1+1 = 10となるので、1ビットの加算を行う場合は繰り上げのある場合を考慮して出力を2ビットにする必要があります。
字汚くてすんません。
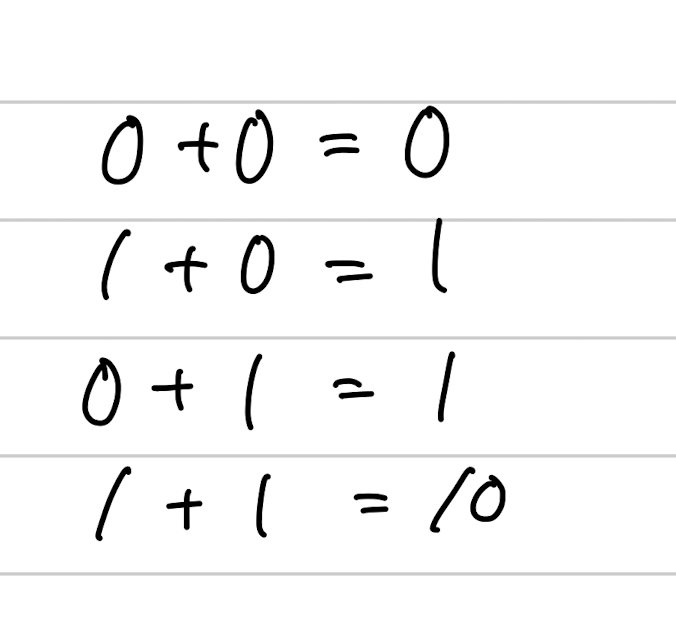
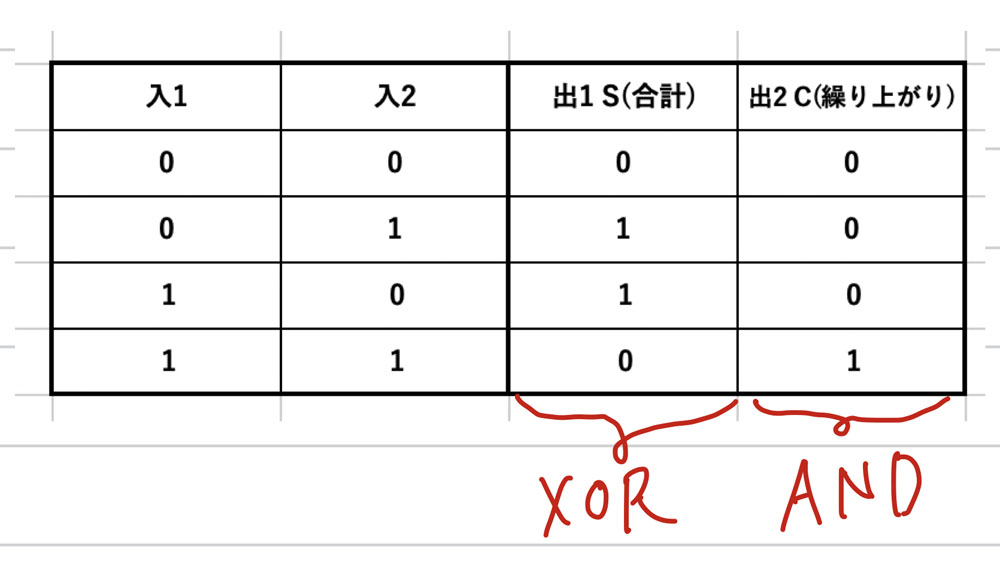
ここで出力を2ビットにして真理値表を見てみましょう。0+0 = 0, 1+0 = 1, 0+1 = 1, 1+1 = 10からわかるように、出力の下位桁はXOR、繰り上がりはANDを取れば良いことがわかります。
よって、MIL記号で書くとよく見る半加算器の形になりますね。
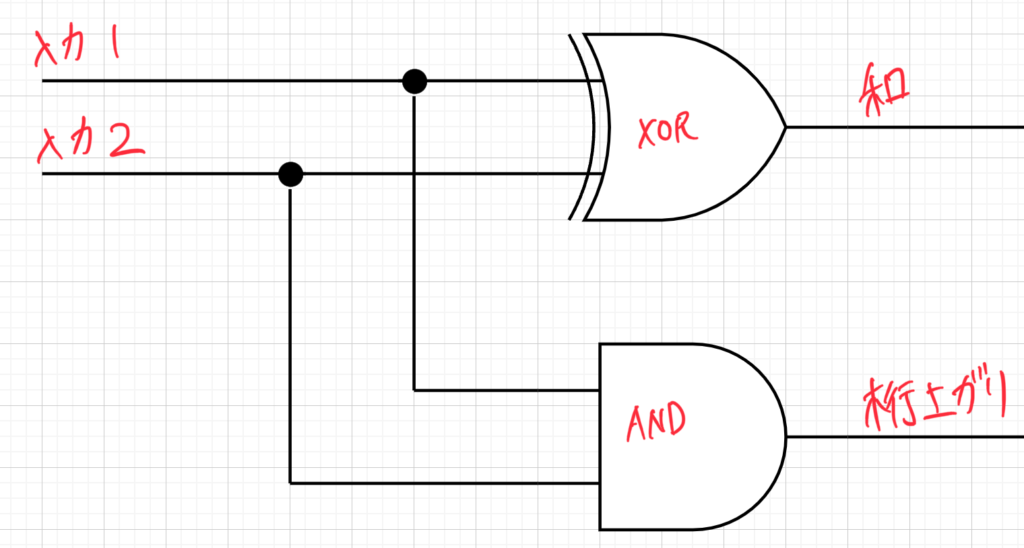
これをマイクラで実現するとこんな感じ。


ちゃんと真理値表と同じになっていることも確認できますね。
ただ、これではスペースを取りすぎるので、今後のためにこれを小型化しておきます。
このように回路を作ると先程の半分くらいのスペースで作れます。

これで、1ビットの加算をマイクラで作れるようになりました。
ただ、1ビットならこれだけで良いんですが、2ビット以上の加算となると下位桁からの繰り上がりを考慮する必要がありますね。これを想定したものが次に紹介する全加算器です。
・全加算器による加算回路
全加算器は先程と違い、加算元2つそして、下位桁からの繰り上がりの合計3つを入力とします。つまり3入力2出力。これが唯一の違いですね。
一見” ただ入力が1つ増えただけ ”の全加算器ですが、基本回路で実現しようとなると意外と複雑になったりします。まずは真理値表から見てみましょうか。
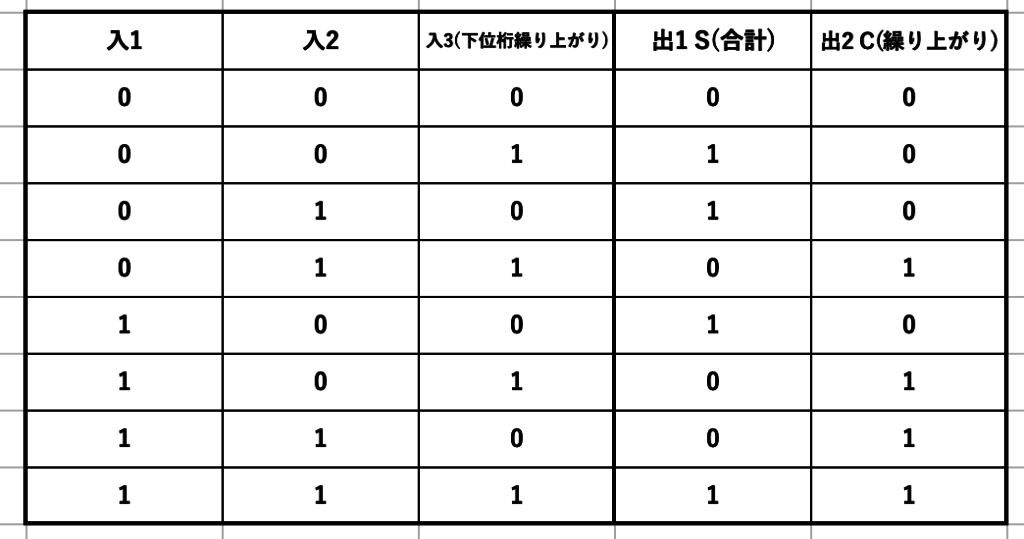
結構大変でしょう?入力1つ増えるだけで2倍の通り数考えないといけなくなります。
先程の話的に繰り上がりはなんか特別な扱いをしなければならないと思う人がいるかもですが、そんなことは無いです。他の入力と全く同じように扱えます。
さあ、これをどう実現するかですね。先に答えを言うと半加算器を2つ用いて実現します。MIL図見たほうが早いかな。

ではこれを実際にマイクラで作成して視覚的に理解してみましょう。ここからは入出力のパターンが増えるので全パターンは載せません。自分で作って確かめてみてね。
(※ 3入力一度に扱えばいいじゃんと思った人へ 論理回路の授業とかで何気なく3入力ANDとか扱ってたりしますが、実用的にはコストの面であまり使われてはいないと思います多分。)
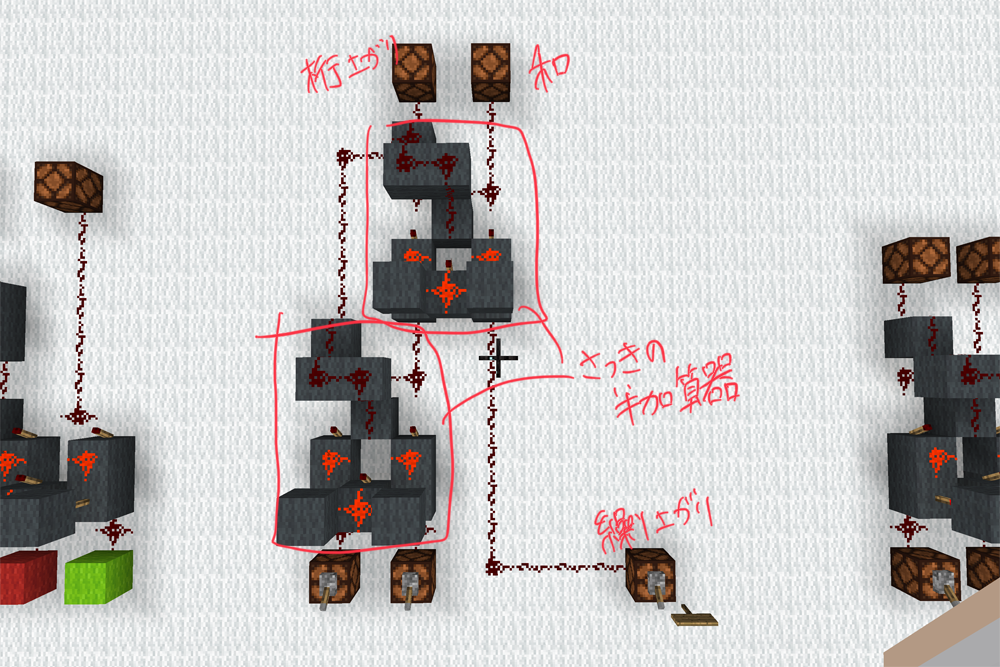
これで繰り上がりを考慮した加算機ができました。
繰り上がり入力を実際に他の加算器の繰り上がりと接続することで2ビット以上の加算を実現できます。最下位桁の加算だけ繰り上がりの入力がないので半加算器になる点だけ注意。
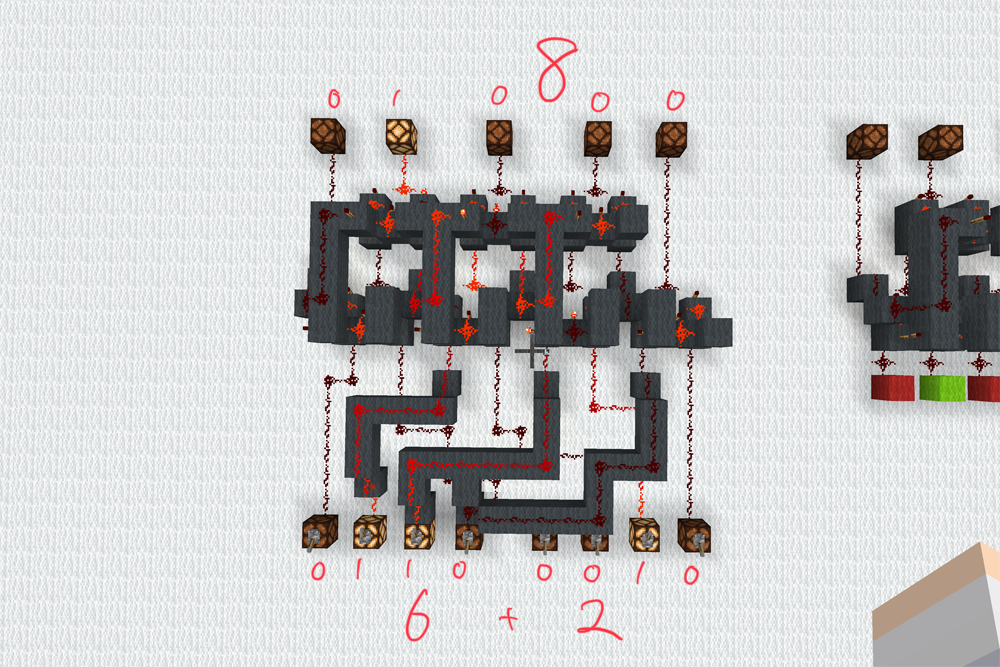
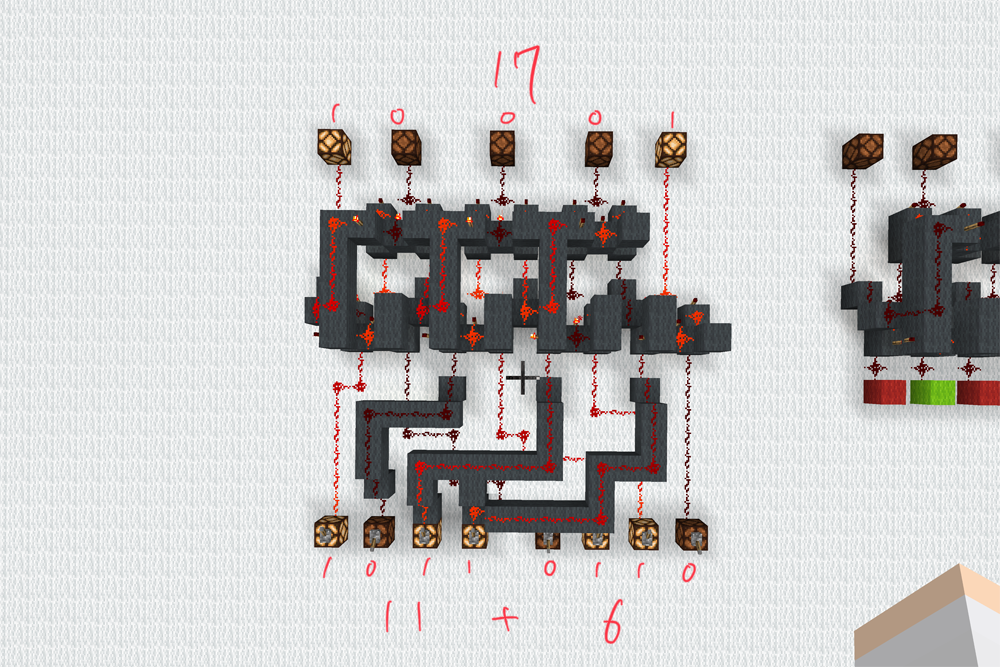
3ビット加算器を作ってみました。出力は4ビットです。

赤の部分が加数で緑の部分が被加数で、右の方が下位ビットです。ただ、これだとちょっと分かりづらいので

このようにして加数と被加数を左右に分けてみました。実際に2パターンほど計算してみましょう。
これにて加算回路完結。次は引き算いきましょう。
・補数の扱い
さて。減算回路を作る前に、まずは補数についての理解が必要です。
既にご存知の人も多いと思いますので簡単に説明しますね。補数とは「ある自然数をn進数で表現したときに、足し合わせるとちょうど「nのべき乗」か「nのべき乗-1」になる自然数のうち、最小のもの」とされています。
つまり、足すと桁が1つ上がる数のうち最も小さい数、ということです。これだけじゃ分かりづらいので例を用いて説明します。例えば、10進数の時、7の補数は3となります。7に何かを足した時桁が上がるような最小の数は3ですよね。
これを2進数で考えてみましょう。1011の補数はどうなるでしょう。
初めて桁があがるということは、次のような式で考えることができますね。
1011 + xxxx = 10000
ということは、
xxxx = 10000 – 1011 = 0101
といった感じで2の補数を求めることができます。
教科書とかでよく書かれているやり方として「各ビットの反転+1」というものがありますが、1011 → 0100
0100 + 1 = 0101となり、ちゃんと同じになることもわかりますね。証明手順知りたい人は参考書へどうぞ。
簡単に補数への変換についてまとめると以下の様になります。

補数への変換ができるようになったところで、今度は最上位ビットの扱いについて話しておく必要があります。先程の2の補数ですが、実は最上位ビット(符号ビットと呼びます)、つまり一番左側の桁はマイナスの桁として扱います。例を見たほうが早いでしょう。
0101は、4 + 1 = 5でしたね。
1010は、最上位ビットのみマイナスとして扱うので補数表現においては、-8 + 2 = -6となります。このように、最上位ビットをマイナスとして扱うことで、負の数も簡単に表すことができちゃいます。実際にコンピュータもこの表現方法を使ってます。
ここで、1つ大事なポイントがありまして、実はこの補数表現において、補数を取るということは、ある数字の符号を反転させるのと同じ操作になります。
例えば、11 = 01011ですよね。これの補数をとります。
01011 → 10100 (ビットの反転)
10100 + 1 = 10101 (+1)
となり10101を10進数に戻すと-16 + 4 + 1 = -11となり、符号のみを反転できたことがわかります。たまたまでは無くすべての数で使えます。
では、実際に補数に変換する回路をマイクラで作って見ましょう。
補数の変換方法は「ビットの反転+1」でしたね、これをそのまま作ってみます。

さっきの全加算器を4ビット+1ビットに変更して、4ビットの入力の前にNOT演算を挟むだけです。1ビットの方は補数を取るときの+1する部分です。なのでここは1固定です。
・補数と全加算器による減算回路
さて、これが何に使えるのかについて話してませんでしたね。結論から言います。補数を使うと全加算器だけで減算を実現することができます。例えば、14 – 6 というのは14 + (-6)のように、減算というのは負の数の加算と言い換えることもできますね。ここで、負の数は先程の補数表現を用いることで表せますし、加算は全加算器を用いればいいです。つまり補数を使えば新たな回路を作る必要が無いということです。
では、全加算器を補数表現で考えてみましょう。
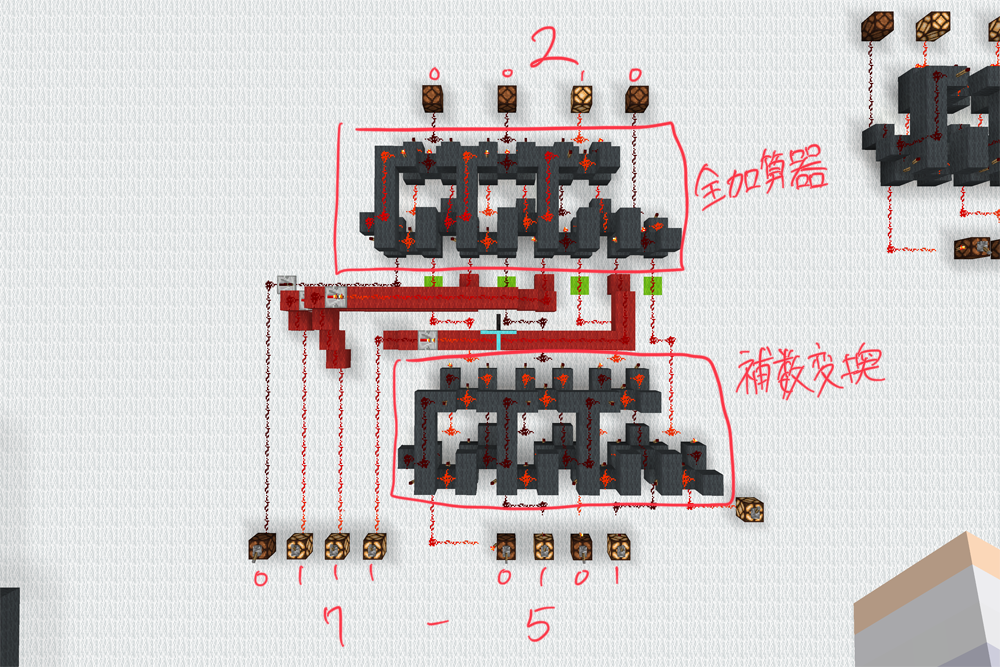
このように、補数表現を使うことで簡単に減算回路を実現できることがわかりましたね。
今回は加減算についてはこの辺で止めておきますが、加算と減算の仕組みは同じなので、加算か減算を表す制御信号(0なら加算、1なら減算みたいな・・)を用いることによってこれらの演算を共通化した加減算回路を作ることもできます。気になる人はマルチプレクサあたりで検索。
・また明日
ちょっと長くなってしまいましたので、続きは明日にしようと思います。失踪しないようにがんばるます。