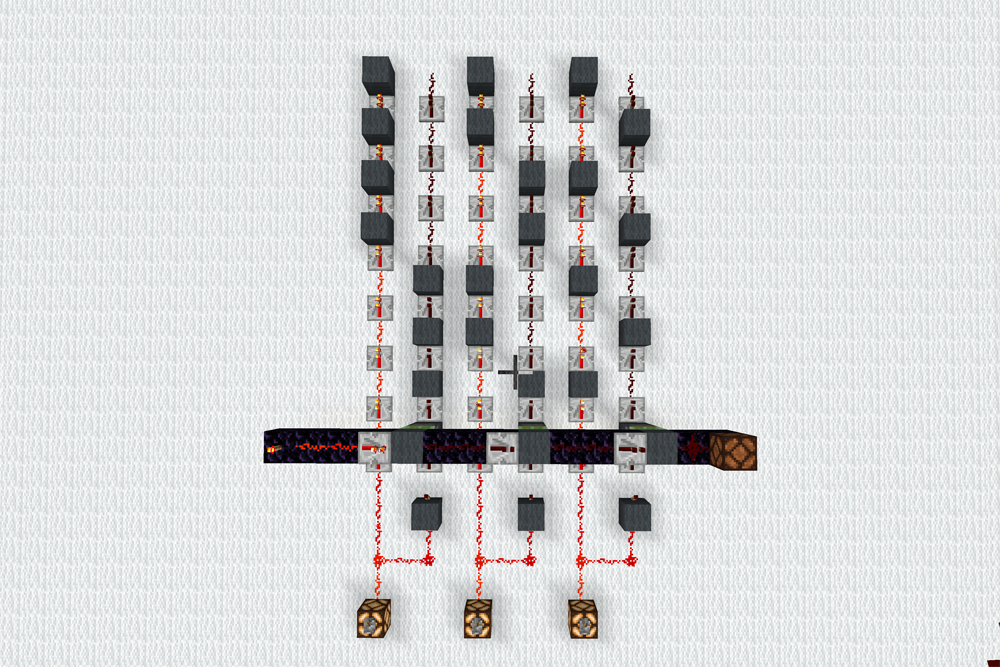
Minecraftで演算回路を理解してみる[2/2]
こんにちは。HayatoIです。昨日に引き続きMinecraftで演算回路を作成して行きましょう。
今日のは少し難易度高めなので昨日の見てないよって人は先に見てくることをおすすめします。
・筆算と乗算回路
乗算回路を見ていきましょう。
乗算を考えるにあたって、2進数の筆算を知っておく必要があります。
人間の世界では、2進数の掛け算は10進数に変換してから掛け算を行う、と習った人もいるかも知れません。しかし、コンピューターの世界では0と1の2進数しか扱うことができないため、掛け算も2進数のまま行う必要があります。
まずは、適当な2進数の掛け算の筆算を見ていきましょう。
上の数を被乗数、下の数を乗数とします。
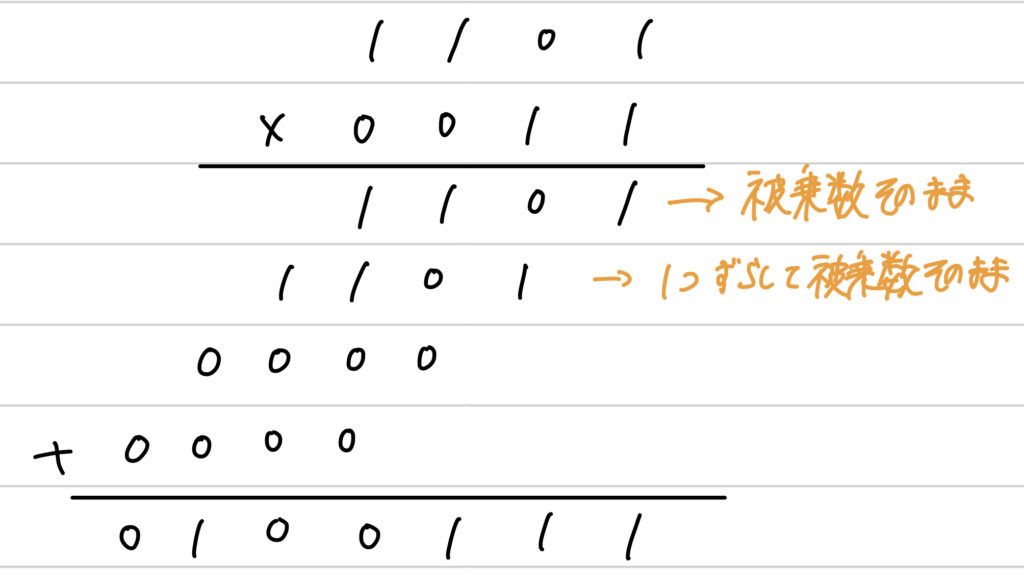
まず、結果の1段目に注目すると、被乗数の値がそのまま出力されていますね。これは、乗数の最下位ビットが1のため、被乗数に1をかけた、すなわち被乗数のそのままの値が出力されていることがわかります。
2段目に注目しましょう。10進数の筆算と同様に桁が一つずれていますが、乗数の下から2ビット目が1のため、二段目にも被乗数がそのまま出力されていますね。
三段目を見てみましょう。乗数の下から3ビット目が0のため、出力は被乗数×0で0が出力されています。
1段ずつ分解して考えることで少しわかりやすくなったのではないでしょうか。
掛け算の方法をまとめると
①乗数を下位ビットから順に見る
②見たビットが1であれば被乗数の値をそのまま出力、0であれば0を出力
③見たビットが下から何桁かを数え、その分だけ先程出力した値を左シフトする
④これらの値をすべて足す
シフト演算については割と奥深いので、詳しく知りたければ各自で調べてみてください。ここでは「桁を左にずらすんだな」程度の理解でOKです。
理論的な理解ができたところで、実際に作っていきましょう。実はこの乗算回路、理論的には割と簡単なんですが、実装が結構大変です。
先程の手順をMIL図で描くと以下のようになります。4×4ビットってのもあるんですが、かなり複雑に見えますね。FA というのは昨日作成した全加算器のことです。
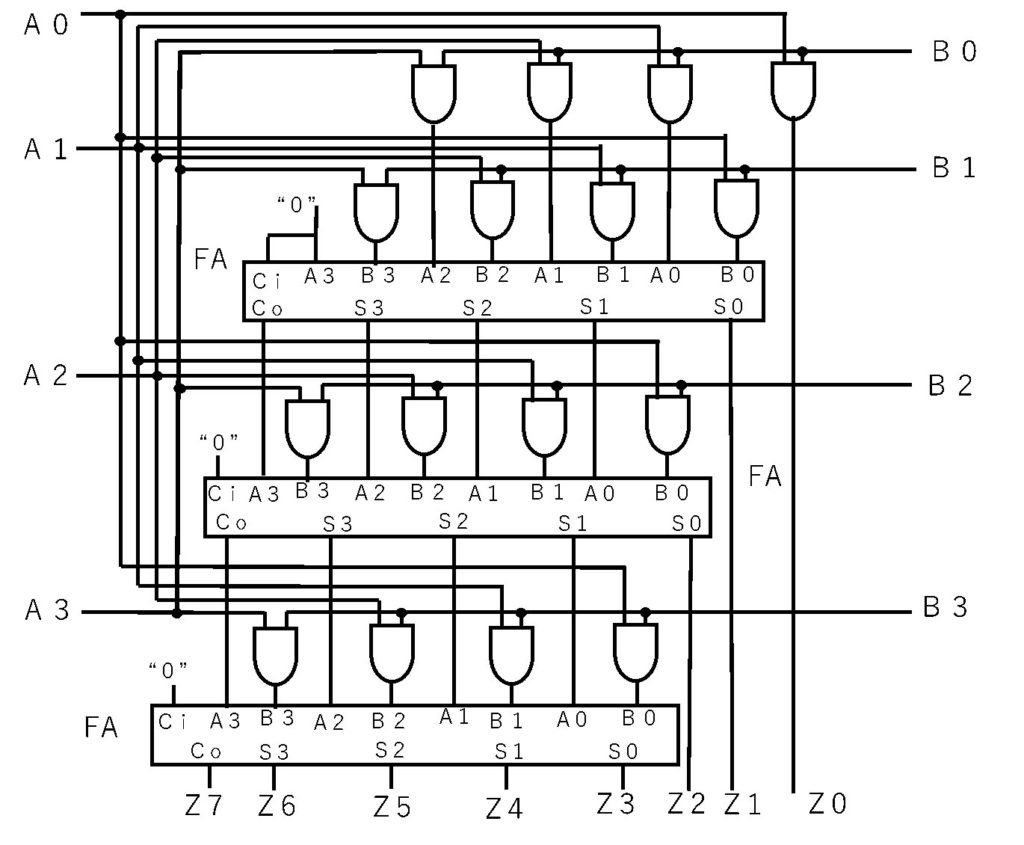
とりあえず図のように作ってみましょう。
これだけじゃ分かりづらいと思うので2ビットの場合を図で書いてみました。

内部はこういう感じになってます。番号振っておいたので、順番に見ていきましょう。
①の部分では、被乗数1桁目と乗数1桁目の演算をしています。先程の筆算の考え方からわかるように、ここでは乗数の1桁目が1だった場合、被乗数の値をそのまま出力すれば良いんでしたね。乗数が1の場合でも、被乗数が0であれば出力は0になるので、この部分はANDを取るだけで良いことがわかります。
②の部分でも①と同様に被乗数2桁目と乗数1桁目のANDを取るだけです。
③の部分は、被乗数1桁目と乗数2桁目ですね。乗数2桁目ということは、一つ左にずらしてから計算する必要があります。なので①とは違って計算前に被乗数1桁目の値を左側に持っていき、乗数2桁目のところでANDを取っています。
④は足し算をしています。②と③のAND演算は、出力の2桁目に相当する演算でしたね。なので筆算と同様、この2つの結果を足してやる必要があります。多分これは図左側の筆算部分見たほうがわかりやすいかも。加算器を用いてXORで2桁目の出力、ANDで次の桁への繰り上がりをしています。
これを繰り返すことで4×4ビットの乗算回路を実現しています。
ちゃんと動作するか試してみましょう。
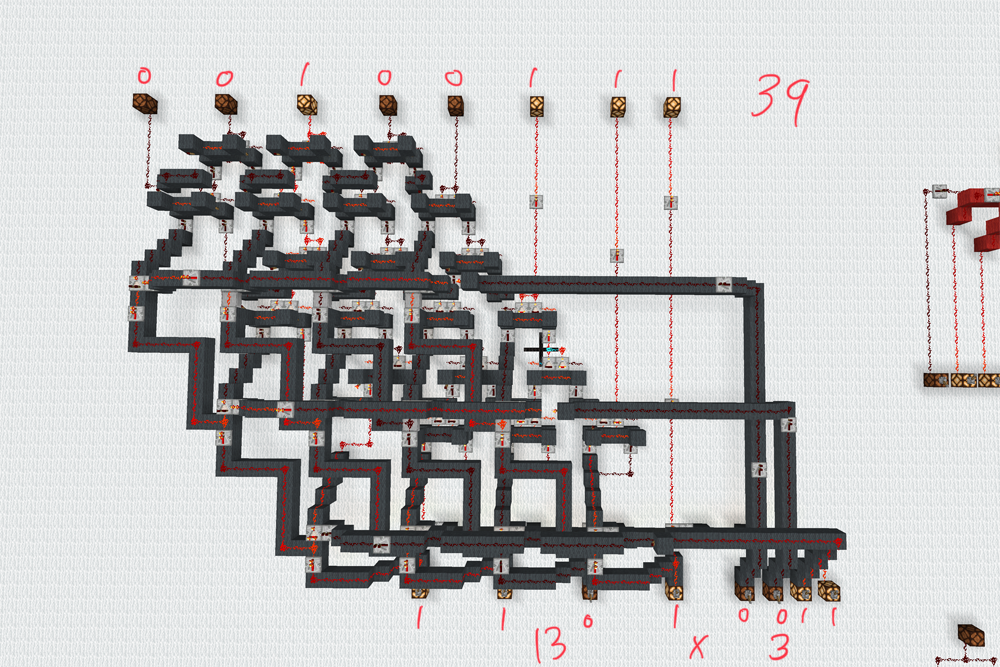
ちゃんと乗算ができていることがわかりますね。実際のCPUはシフト演算でループしながら計算していくのですが、これをマイクラで実装しようとするとメモリ関連の知識も必要になってきてかなり面倒なので今回は勘弁してください。気になる人は「掛け算 シフトレジスタ」辺りで検索。
オーバーフローがなければ一応この回路で補数を扱うことも可能です。
・除算回路
四則演算もいよいよ最後、除算回路。割り算ですね。四則演算のラスボスにふさわしく、難易度かなり高いです。
・・・・・・・・すんません。時間足りませんでした。
回路の内容まで話すと3日くらいかかっちゃいそうなので簡単に考え方だけ話そうと思います。
割り算も掛け算と同じく基本的に筆算で考えていきます。
ただ、掛け算のように「ここが0ならこう、ここが1ならこう」と決めることができません。例えば、商の部分ですが、割り算は上から計算していくので商の最上位ビットから見ていきましょうか。
商の最上位ビットですが、ここには0か1が入りますね。これをどうやって判断すればいいでしょうか。少し複雑なんですが、被除数の最上位ビットから除数を引けるかどうかで判断することができます。
つまり、(被除数の最上位ビット) – (除数)の計算をして、その結果が0以上なら商の最上位ビットを1、そうで無ければ0にすれば良いというわけです。
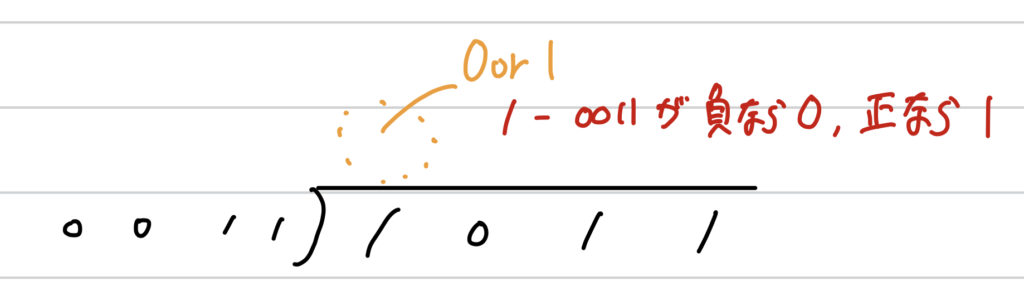
その後、0がたった場合は被除数の最上位ビットとその次に大きいビットをそのまま下ろします。1がたった場合は(被除数の最上位ビット) – (除数)の結果に被除数の2番目に大きなビットを加えてから下ろします。(1がたった場合なので(被除数の最上位ビット) – (除数)の結果は必ず0以上)
これを被乗数のビット数分だけ繰り返します。
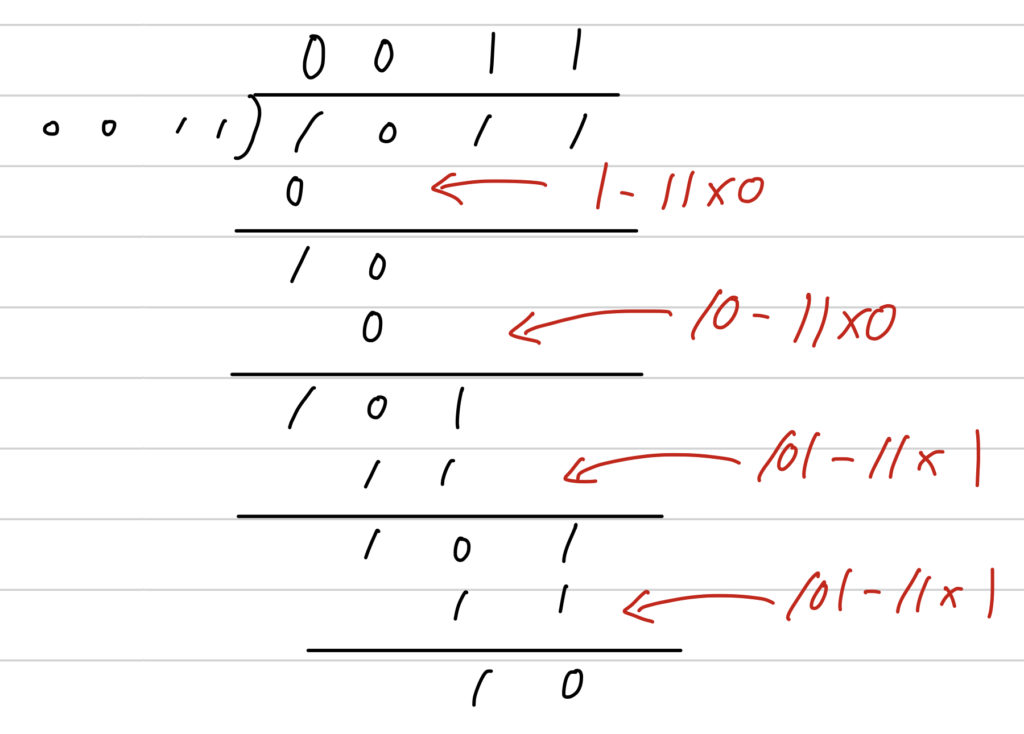
一応作りました。もう作りたくないです。
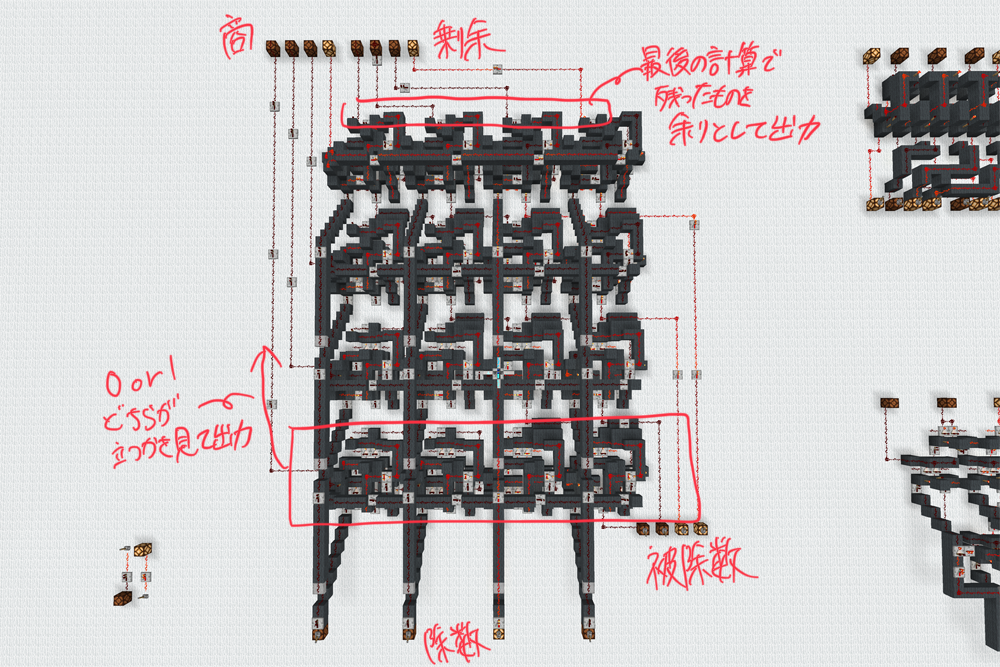
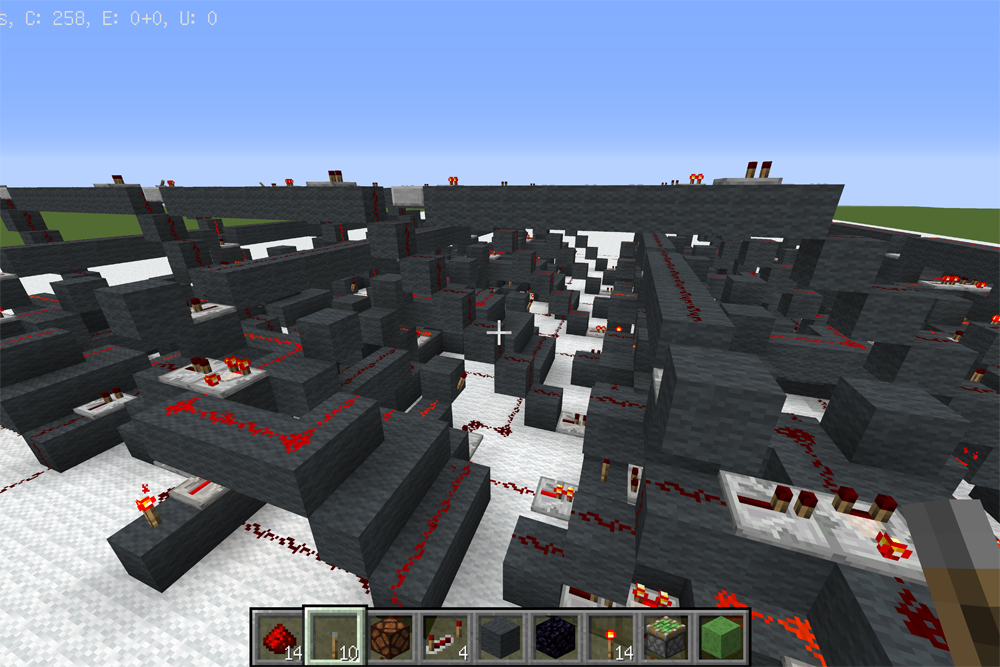
図見ればある程度はどこでしてるか理解できると思います。回路のかたまり?ブロック?のようなものが4つありますが、そこでそれぞれ先程言った引き算をし、商に0か1のどっちが入るのかを見ています。0の場合はそのまま次(上)のブロックへ、1の場合は引き算した結果を次のブロックへ移してからそれを1ビット左に移し、被乗数の次の桁を加えています。
そして4回繰り返し、最後に出力されたものをそのまま剰余としています。
動作確認してみましょう。
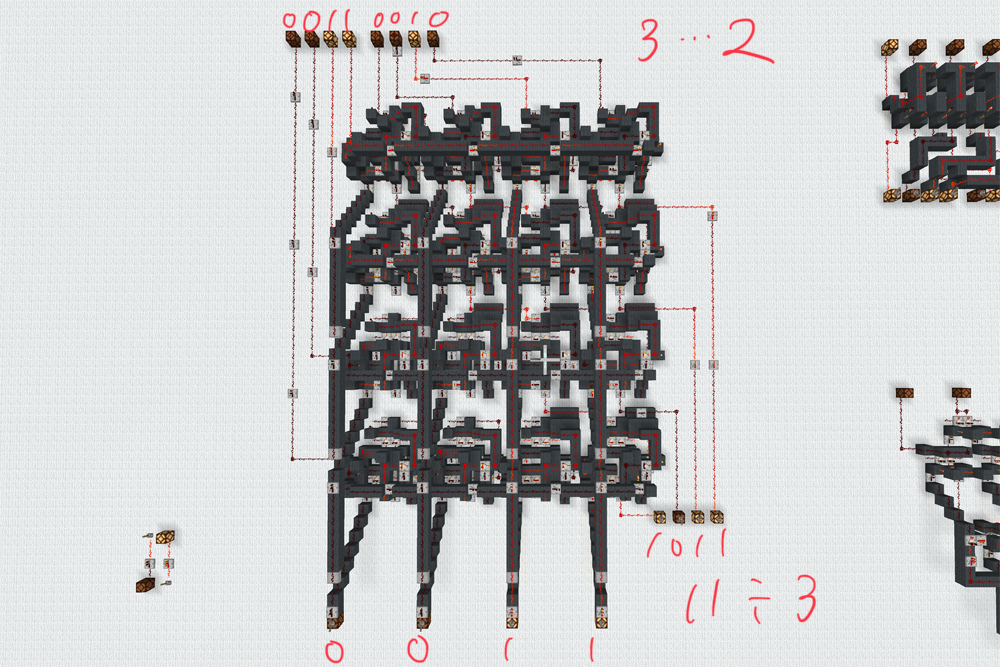
さっきの筆算と同じ結果になりましたね。大丈夫そうです。
割り算に関してはこれくらいにしておきます。
・エンコーダ、デコーダによる2進数⇔10進数変換
では、最後に2進数⇔10進数の変換を実装して終わりましょう。そんなに難しくないです。
ここまでで足し算や引き算など四則演算の演算回路は一通り説明してきましたね。しかし、これらは2進数によるものなので10進数で生活している私達には少し扱いづらいです。先程から言ってますがコンピューターは2進数しか扱うことができないため、電卓などを作成する際は2進数を10進数にしたり10進数を2進数に変換してあげる必要があります。
そこで使われているのがエンコーダ、デコーダです。エンコーダは10進数を2進数に変換するもので符号器とも呼ばれます。デコーダはその逆で2進数を10進数に変換します。復号器とも呼びます。恐らく次の図を見てもらった方がわかりやすいでしょう。実際の電卓計算などではこんな風になってます。

役割を理解したところで、次はこれらの仕組みを考えながら実装していきましょう。
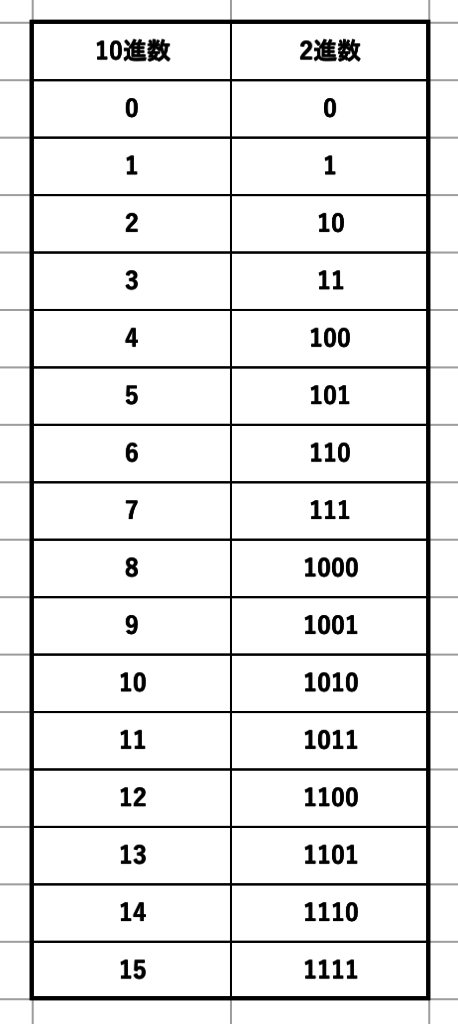
10進数と2進数の対応表です。これは流石に大丈夫かな。言ってしまえばこの対応表のようになるように回路を作成すればOKってわけです。
まずはエンコーダから。ここでは入力を0~7までの10進数とします。その場合出力は3ビット用意しておけばいいですね。入力の10進数は8本線を用意し、それぞれに0~7を割り当てます。この8本の線は2つ以上同時にONになることが無いので真理値表は次のようになります。

真理値表から、出力Z1 = A1or A3 or A5 or A7, Z2 = A2 or A3 or A6 or A7, Z3 = A4 or A5 or A6 or A7ということがわかります。これをそのまま実装してみましょう。

左側にあるのが入力で縦のラインが出力になります。ここから上手いこと入力に対して出力ができるようにします。
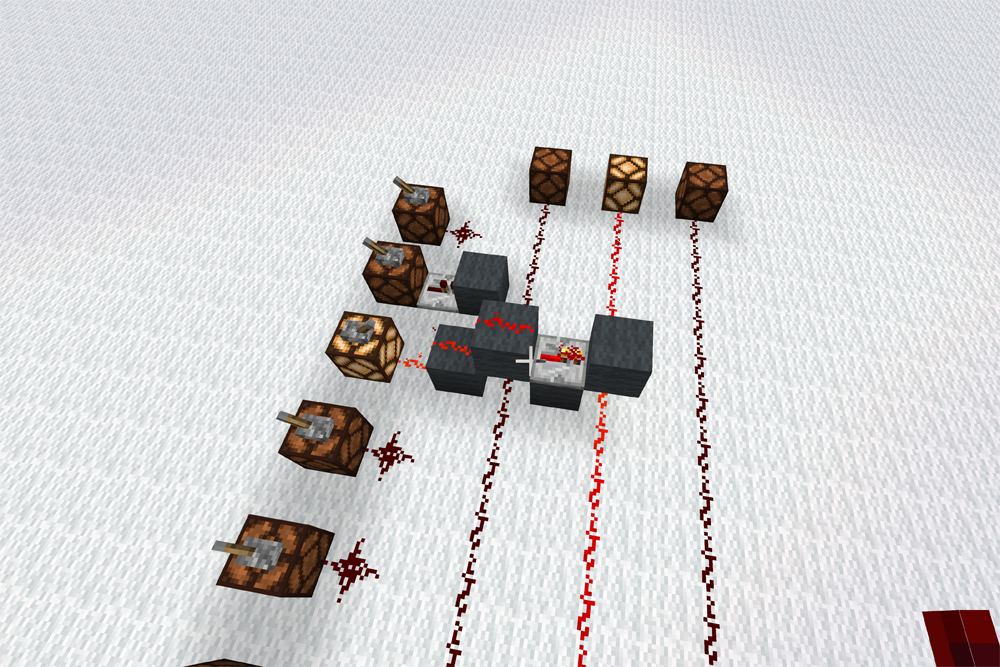
例えば2を出力したい場合、このようにすればOKです。ちゃんと2ビット目だけ光ってますね。ここは少しマイクラ力が問われます。
0~7まですべて作るとこんな感じです。

ちょっと前に論理回路は基本2入力にしてねと言ってた気がしますがOR回路はこれでできてしまうのでこれで作っちゃいます。
実際に試してみましょう。
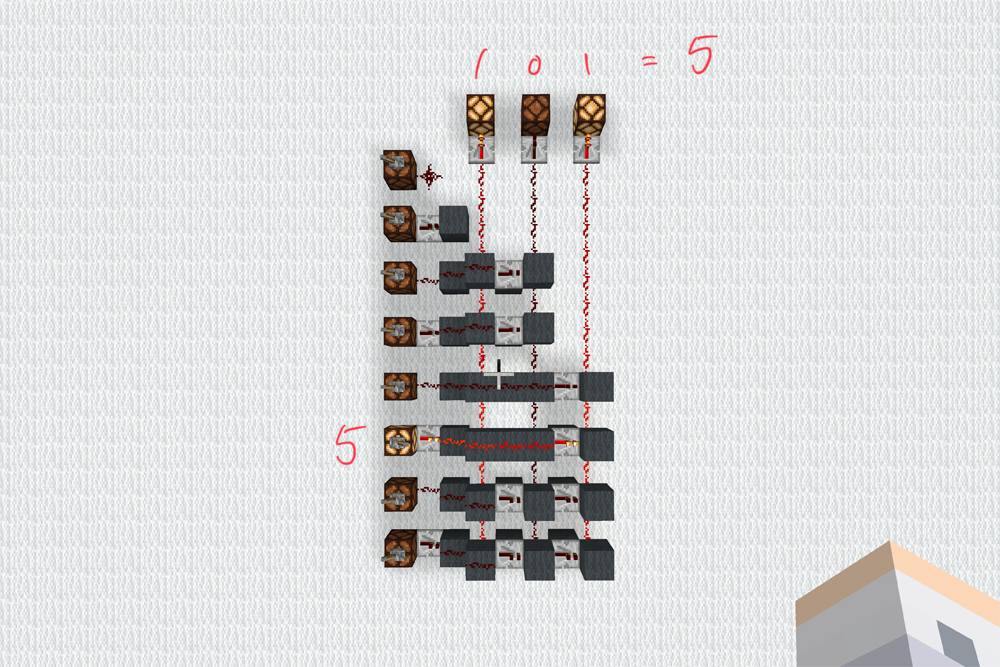
エンコーダ完成。これだけ。
次はデコーダ。さっきの真理値表の入出力を反転させます。3入力8出力となりますね。

この真理値表から、Z0 = notA1 and notA2 and notA3, Z1 = A1 and notA2 and notA2 ・・・となります。
これを実装してみます。NOT演算を多用するので、最初にこのようにNOTに分岐させて6本の線を引くと楽です。そこから必要なものを取り出してAND取るだけ。

ANDを取るために少し特殊なアイテムを使います。「ピストン」と言うアイテムでレッドストーン信号が入力されることで上下に伸縮します。これを真理値表と照らしながら適当な位置に置きます。
これを0~7まで全部作ってみるとこんな感じ。

一部特殊なブロックがありますが気にしない。
動作確認してみましょう。
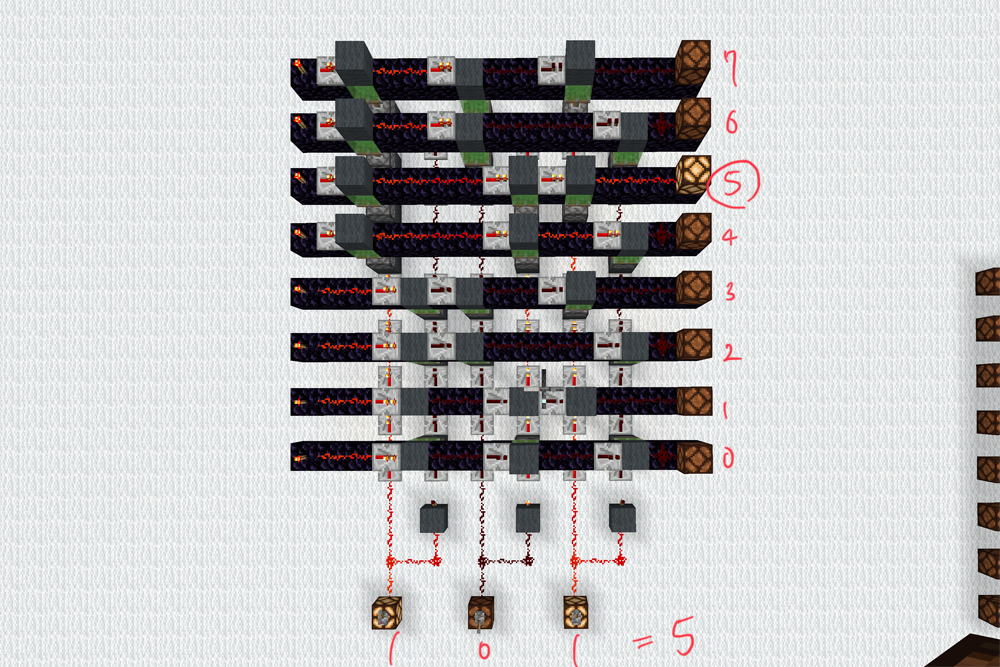
大丈夫そうですね。
これで
10進数入力→2進数変換→四則演算→10進数変換→10進数出力
という一連の流れができ、私達にも扱いやすくなりましたね。
マイクラで電卓を作るような猛者たちはこれをベースに、桁数を増やしたりボタンによって演算の種類を変える回路くっつけたり7セグメントでディスプレイ出力回路作ったりしてる訳です。
・さいごに
ちょっと長くなりましたが2回にわたってマイクラで演算回路を作ってみました。少しでも論理回路についての理解を深め正課の授業などに役立てば幸いです。
今回は四則演算、基数変換だけでしたが、気が向いたらメモリや順序回路なんかについても書いて見るかも(多分書かない)。ほんとマイクラって何でもできるんですよ。図描くのと違って10倍くらい大変ですけど、完成したときには達成感と共に理解がかなり進みます。冬休みの暇つぶしに是非。え?Logisim?何それ??
以上、特に論理回路が専門でもない実世界コース2回生のHayatoIが2日間にわたってお送りしました。
最後まで見てくださりありがとうございました。
参考にしたサイトや記事は以下の通りです。