扇状に弾を発射したいんだ！

この記事は何

この記事では、弾幕ゲームなどを作る際に生じる、等間隔に扇状に弾を発射する方法について説明します。三角関数の$sin$と$cos$の定義がわかる方で、四則演算をする根気があれば難なく理解できると思います。(三角関数の定義を理解していたら多くの方はこれを自力で導き出せると思っています。)

記事の最後には動作例もあるので是非見てくださいね。

ご挨拶

みなさんこんにちは。RiG++コーディング課の田きです。またお前かよ！と思う方もいらっしゃるでしょうが私は気にしないので大丈夫です(？)。とはいえ、誰であろうときれいな模様について考えているときは不安から逃避できるので、きれいな模様を描くための初歩的な話をしていきたいと思います。

今回やる事

この記事では、Unityエンジン上で扇状の弾幕を作っていこうと思います。その方法を書いていこうと思います。

登場する変数

弾の数($n$とします)

弾と弾の角度間隔($θ_{distant}$とします)

実際に考察してみましょう

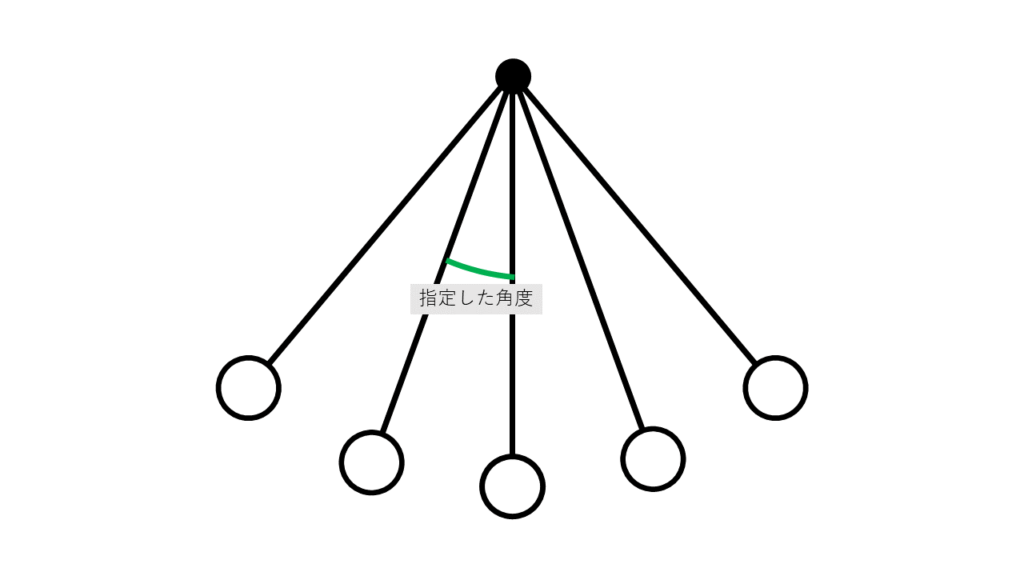
$n$個の弾を、角度を $θ_{distant}$ ずつずらして扇状に発射することを考えます。少し考えると、明らかに、以下のようにすると円状に発射することができます。

$弾_i$の速度を$v_i$とします$(0\leqq i<n)$。この時、$θ_i = θ_{distant} *i$とすると、 $v_i= (cos θ_i,sin θ_i)$と表せます。

上の内容が言っているのは、i番目の弾は、$i$の数と$n$の数に応じていい感じに開店した方向に発射してね、という内容です。そうです。円状に発射する時と同じ説明です。当然、for文で簡単に表すことができます。弾の速度はUnityの物理演算機能に任せちゃいましょう。そうすると簡単です。

ちょっと改善してみましょう

しかし、上の例であると、角度の中心は$i$=0番目の弾となってしまいます。そのため、角度が正の方向に偏ってしまいます。そのため、角度を補正しましょう。

扇型の持っている角度の大きさは、$(n-1)* θ_{distant} $となっています。これだけの量がすべて正の方向になので、これを是正するために、$(n-1)* θ_{distant}$ の半分を引きましょう。すると、正負の方向に等しい角度となります。

そのため、上の内容を改善すると以下のようになります。

弾_iの速度を$v_i$とします$(0\leqq i<n)$。この時、$θ_i = θ_{distant}*i – (n-1)* θ_{distant}/2$ とすると、 $v_i = (cos θ_i,sin θ_i)$と表せます。

これで、弾の方向の偏りを解消することができました！

まとめ

わりと簡単に扇状に弾を発射することができました。すこしだけ考察要素も出てきましたが、そこまで難しい内容ではありませんでした。

扇状に弾を発射するのは弾幕の基本です。前回同様、示した式を少しいじるだけでもバラエティに富んだ弾を発射することができます。また、円状に発射する弾幕と組み合わせてもいい感じになるかもしれません。

弾幕を楽しんでくださいね。

動作例

拙作ではありますが、以下のようなものが作れます。

上の動画では、徐々に徐々に弾の間隔が狭まっていくような工夫がされています。これだけでも動きがあって面白いですね。